Decision Modeling and Optimization in Game Design, Part 6: Parametric Design Techniques

This article is the sixth in a continuing series on the use of decision modeling and optimization techniques for game design.  The full list of articles includes:

• Part 1: Introduction (Blogspot) (Gamasutra)
• Part 2: Optimization Basics and Unrolling a Simulation (Blogspot) (Gamasutra)
• Part 3: Allocation and Facility Location Problems (Blogspot) (Gamasutra)
• Part 4: Competitive Balancing Problems (Blogspot) (Gamasutra)
• Part 5: Class Assignment Problems (Blogspot) (Gamasutra)
• Part 6: Parametric Design Techniques (Blogspot) (Gamasutra)
• Part 7: Production Queues (Blogspot) (Gamasutra)
• Part 8: Graph Search (Blogspot) (Gamasutra)
• Part 9: Modular Level Design (Blogspot) (Gamasutra)

The spreadsheet for this article can be downloaded here: link

Introduction

In the previous articles in this series, we introduced the concepts behind decision modeling and optimization and explained how they can be helpful in framing and optimizing a surprising number of design decisions.

We also discussed their limitations, and we showed a number of examples of how they can be used to find optimal player strategies in certain cases and to help optimize design decisions directly (see links above).

In this installment, we're going to slow down a bit, and simplify.

We're also going to get much more practical, and how how you can use a very simple decision model to frame certain kinds of parametric design problems.  We'll also discuss the broader practical applications of this approach, including how we used this approach in our recent iOS/Android strategy game, City Conquest.

Designing Towers

Imagine for a moment that you want to design a tower defense game.  You know that you have enough production resources available to create 8 unique towers.  How do you go about framing the problem and deciding the best set of 8 towers to include in your game?

Obviously, you could just go and come up with a bunch of ideas for towers, and then just pick the best out of that group.  That's a start.

Or maybe you could look at some existing tower defense games, like FieldRunners and Kingdom Rush or any of the popular tower defense mods for StarCraft 2, and then experiment with variations on the towers in those kinds of games.

But that's not a very disciplined approach, is it?

If we're just coming up with random ideas, how do we know we haven't randomly chosen a lot of bad ones, or that we couldn't have randomly chosen a bunch of better ones?

When we design our towers, how do we give ourselves some sort of disciplined basis for deciding that one tower design is better than another?  And how do we know that once we've got our set of 8 towers, that the configuration we've chosen is the best set of 8 towers for our game?  Is that even possible?

For that to happen, we'd have to invent some definition of "best" in terms of how appropriate they are for our game, how interesting they are, and how well they suit our design goals.

Obviously, that's a bit of a stretch.  That kind of definition of "best" isn't going to be something we can encode in any sort of function.  And there's obviously no way to have a spreadsheet pick out how "interesting" something is; that's a judgement call and we'll have to do it ourselves.

Let's take a step back.

In an ideal world, our process for picking the towers should probably look something like this:

• First, we'd explicitly specify our design goals.  We'd write down on a sheet of paper exactly what we're trying to accomplish with the design of our towers.  This forces us to clarify our thoughts about the design up front so that we don't go rushing into the tower design problem recklessly and have the bigger picture in mind.
• Then, we'd set up some sort of framework for making the tower design decision, so that we're designing the full set of towers as an organic whole rather than taking a bunch of towers that were designed separately and throwing them all together.

Our design goals could include things like uniqueness (every tower should be significantly different from all the others and should play a unique tactical role), usefulness (there should be some situations where each tower is the most useful), and balance (every tower should be appropriately powerful and should have a cost appropriate for its utility).

(You can find a partial list of my own design goals for my recent iOS/Android game City Conquest in the February 2012 interview on AiGameDev).

So, let's assume we've done that, and we have our goals clearly defined on an 8.5"x11" piece of paper.  How do we then define a framework for the design decision?

Design Parameters

If you look at tower defense games that have a large number of tower types, such as the excellent Element Tower Defense mod for StarCraft 2, or if you look at a large number of tower designs across a broad selection of tower defense games, you'll notice a clear pattern.  All of these tower designs seem to be based on a combination of parameters: they have some method of applying damage, and apply some number of effects, such as damage or healing or slowing.

This is very similar to the way I approached the design of the towers in City Conquest.  Even though City Conquest is more of a tower defense / real-time strategy hybrid, the tower design is similar enough to a tower defense game that it's worth considering.

The image below shows some of the different towers available in the game.  The full set of towers was designed together, as a whole, by matching different attack mechanisms with different effects as we describe in this article, in order to ensure that they were as unique as possible and satisfied our design goals.

For example, along the top row of the image, we have the Chiller Unit (upper-left, which emanates slowing in a radius around itself), the Laser (which fires slowly and damages units in a long, straight line), the Grenade Tosser (which lobs ground-to-ground projectiles that do wide area damage on impact), the Gun Turret (which fires rapid plasma bursts at air and ground targets), and the Missile Launcher (which fires homing missiles at air and ground targets and does a small amount of radial area damage in addition to its direct damage).

Each tower can be viewed as having two fundamental parameter types:

• A mechanism of action.  This defines the way the tower applies its effect to the enemy units (or, in some cases, to friendly units or to other nearby towers).
• An effect.  This is what the tower actually does, and what sort of damage or healing or anything else that it actually applies.

Mechanisms could include things like the following:

• Instantaneous shot
• Ground-to-ground projectile
• Ground-to-air projectile
• Homing projectile (can target both air and ground; seeks to target)
• Circular blast around tower
• Electric arc (hits multiple nearby units in sequence)
• Conical spray
• Linear beam (fires over any number of tiles in sequence along a straight line)

Effects can include things like:

• Fast direct damage (i.e. rapid fire against a single unit)
• Slow direct damage (i.e. heavy fire against a single unit with a long cycle time)
• Direct damage + area-of-effect (AoE) splash (i.e. damage against a single unit with a small amount of splash damage against other units nearby)
• Area of effect (AoE) damage only (shockwave)
• Slow: slows affected enemy units for a short period of time
• Stun: stops affected enemy units for a short period of time
• Weaken/debuff: weakens affected enemy units for a short period of time so that they take more damage from all sources while affected by the "debuff"
• Absorb health: absorb some of the unit's health and apply it to this tower
• Remove buffs: remove any special "buffs" from the affected unit, such as any speed or health or damage enhancements
• Push back: push the unit backward a short distance

(This is only a partial list, of course; we could have any number of "effects," such as turning units invisible, turning them into zombies, or what have you.  This list is only for the sake of the example and the reader is invited to make up his or her own list as needed.)

We should be able to define our towers as a combination of one mechanism and one or more effects.

If we do this, the question then becomes, which towers get which mechanisms and which effects?

Once we answer that question, we'll know each tower's role in the game, and this defines its personality, and we can then use that to determine the tower's visual style and start working on concept art.

We have 8 mechanism types, and 10 effects.  So each tower will have one of the 8 mechanisms and one of the 10 effects, but 2 of the effects will go unused.  That's fine.

Of course, there are lots of other ways we could do this, such as by giving each tower multiple effects or allowing it to change mechanisms or effects over time, but for the sake of brevity we'll leave those as an exercise for the reader.

Applications

Of course, the point of the article isn't about tower defense games; it's about modeling decisions.  These are all sorts of situations in game design where we need to design a large number of entities in particular functional roles.  For example:

• Designing buildings or units in a strategy game
• Designing guns, vehicles, or enemies in a first-person shooter
• Designing creatures and character classes in a MOBA (multiplayer online battle arena) action game
• Designing spells, enemies, character classes, or loot in a role-playing game

Many games already openly embrace parametric design.  Gearbox Software's Borderlands famously embraced parametric design for its weapons, boasting over 17,500,000 different varieties of weapons due to  the ability to create new guns based on different parameter combinations.  A recent Gamasutra article on the evolutionary system behind Team Blockhead Wars described a similar approach based on 10 parameters for each weapon.

Some might criticize this approach as "slot machine design."  There's some truth to this criticism; this kind of process can easily result in unit/enemy/tower/spell designs that feel rote and formulaic if we're not careful.

But this is not a fundamental problem with the approach itself.  This approach is only a tool, and like any design tool, it has to be used with caution in the context of the broader design to ensure that the parametric design never has a negative impact on the player experience.

In particular, we have to avoid falling into the cognitive trap of assuming that quantity equals quality, or that it necessarily even contributes to quality.  Any number of interesting choices we present the player will always provide a better experience than an infinite number of boring choices.

Tower Design Problem: Setup

Just as with previous articles, we're now going to show you how to model this problem in Excel as a decision model and then use Solver to optimize it.  Unlike the previous articles, though, this article shows what's essentially a subjective design process, where the numbers represent our own opinions as designers.

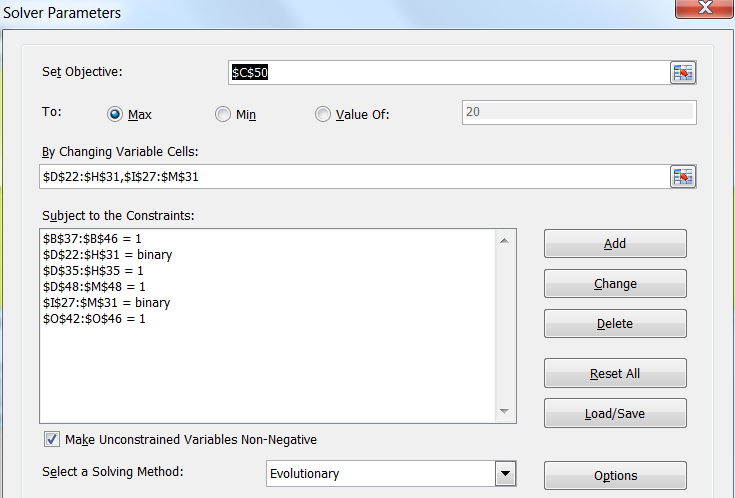
We'll start by simply making a table.  We'll enumerate the towers' possible "mechanisms" along the horizontal axis and the "effects" along the vertical axis.  This is the "Decision Table."

Then, just above that, we make a row of cells: the "Decision Cells."  Since each of the 8 mechanisms has to be mapped to exactly one effect, we only need these 8 decision cells.

We're going to ask Excel Solver to fill in each of these decision cells with a value from 0 to 9 (inclusive) to represent which of the 10 effects they're mapped to.  Since they're the decision variables, we've also highlighted them in yellow, as per our formatting standards from Part 2.

The grey cells in the Decision Table below that simply show a '1' value if the corresponding decision cell (the yellow cell in the same column) equals its row index, or a '0' otherwise.  You can see above that the decision cell values "1 2 3 4 5 ..." result in a down-sweeping diagonal of '1' values.

[At this point, you may be a bit incredulous.  How can we really set up a table to solve this problem?  After all, if there are 8 tower mechanisms and 10 effects in our list, there's a huge number of possible permutations -- if each tower is assigned one unique effect, that's around 1.8 million possible combinations.  Surely we can't search through all of those and find the best one?

But of course, we're not going to do that.  We're just going to use Solver to help us make this decision.  All we really need to do is find the first combination that looks good.  If we don't like what Solver gives us, we can ask it to give us another one.]

Back to the spreadsheet: we now create a second table with a set of weights.  This table will list our own subjective preferences for any given combination of a tower's  mechanism and effect.

We initially fill this table in with '1' values for anything.  As we design our towers, we'll work by changing the values in this table.  A '1' means that the given combination is acceptable and a '0' indicates that it's forbidden for some reason.

For example, we might decide that a particular combination just doesn't make sense, or doesn't satisfy our design goals, so we'd set the weight for that combination to 0.  We might also decide to use this to ensure that our game is too similar to another game -- for example, "Instantaneous Shot + Fast Direct Damage" is too similar to the machine gun tower from FieldRunners, while "Homing Projectile + Slow Direct Damage" is too similar to that game's rocket launcher, so we might set those values to 0.

In the same way, if we've already made up our mind that a certain mechanism/effect combination should be in the game, we can fill in a '1' in that cell and a '0' in all other cells in the same row and column.  This will force the Solver to exclude any other towers from using that same mechanism or effect.

We can also use this table to specify preferences.  A value between 0 and 1 will indicate that the combination is less desirable than another combination, while a value greater than 1 can indicate that it's more desirable to whatever degree.  (You could also think of these as representing relative utilities in utility theory).

Finally, we make a third table that combines the Decision Table with the Weight Table.  This is the Combined Output Table, shown below.

Each of the cells in the Combined Output Table multiplies the corresponding cell in the Decision Table against the corresponding cell in the Weight Table, so that if either of the two values is 0, the resulting value is 0 in the Combined Output Table.

Also, you'll note the columns along the right side of the table, labeled 'Min,' 'Used,' and 'Max.'  The 'Used' column (in grey) count the number of nonzero entries in the corresponding row and column in the table, and 'Min' and 'Max' allow you to set what the minimum and maximum values should be for those values.

Note in particular the implementation of the "Used" column.  Since we can use non-integer weights in the Weights Table, we don't want to use the "=SUM()" formula for this.  Instead, we use Excel's "=COUNTIF(range,">0")" for this in order to count the number of nonzero weights, not sum them up.

In the lower right corner is the objective function.  This cell just sums up the total value of the entire Combined Output Table, and as such, it represents our current preferences in the Weights table multiplied by our design decisions from the Decision Table.  We will ask Solver to maximize the value of this cell.

Tower Design Problem: Solving

Broadly speaking, there are two ways we could approach this problem:

• Try to set the correct weights for every single weight in the Weights Table, and then attempt to solve.
• Set every weight in the Weights Table to 1, run Solver, and then adjust the weights only when we don't like the solution.

Either approach is valid.  However, we're going to take the latter approach because it's quicker.  The former approach forces us to figure out a weight for every possible (mechanism, effect) combination,

Our process will look like this:

1. Set up all the weight values in the Weights Table with weighting values we think are appropriate.
2. Run Solver.
3. Take a look at Solver's solution and figure out if we like the solution it gives us.
4. If not, go through all the tower combinations we don't like, set the corresponding weights for those combinations in the Weights Table to 0, and return to step 2.

This might take a little time.  It might be 5-10 run-throughs before we find a combination that we like.  That shouldn't take long, though; the hard part is just getting the spreadsheet and Solver set up.  Once we do that, actually running it and tweaking the Weights Table will only take a few seconds.

For our initial setup, we have the following, the same as shown above:

The value of the Objective cell is 8, which is the total value of all the green cells (note that we use Excel's conditional formatting here to color the cells inside this table according to their values and make the table easier to read).

This result is suggesting we should have an instantaneous-shot weapon that does slow direct damage  ...  a ground-to-ground projectile that does direct damage plus an area-of-effect ("AoE") splash  ...  a ground-to-air projectile that does AoE damage only  ...  and so on.

Some of these tower designs make sense, but three of them seem a bit silly.

• The ground-to-air projectile that does AoE damage only is probably a bad idea.  This will be the only solely anti-air tower, and we probably want it to do some kind of direct damage so that it can be useful against individual flying enemies.
• The homing projectile with the slow effect is also probably a bad idea.  We'll probably want more enemies to be affected by the slowing effect than what we'd get with a homing projectile.
• The linear beam that removes buffs also seems pretty silly.  This seems like a giant laser weapon that can fire through long groups of tiles at a time, so we probably want that to do direct damage of some sort.

Since we don't like these three tower configurations, we'll set the weights for these to 0 in the Weights Table and run Solver.

(If you can't find Solver or you don't have it installed in your copy of Excel, see the instructions in Part 2 of this series.)

Here's what our Solver configuration looks like:

The decision cells ("By Changing Variable Cells") are the row of yellow Decision Cells just above the Decision Table.  The other constraints in the Solver dialog simply indicate that the decision cells are integer values between 0 and 9 (to represent the 10 possible effects that they can map to), and that all the constraints on the right side of the Combined Output Table need to apply (that is, the values in the "Used" column need to be greater than or equal to the corresponding "Min" values and less than or equal to the corresponding "Max" values).

Now, we hit Solve.

Interesting!  We get completely different results now.  There are still some tower designs that don't make much sense here:

• The ground-to-ground projectile having "Remove Buffs" is a bit silly, so let's set that to 0.
• The ground-to-air projectile having direct damage + AoE splash actually seems like a really good idea!  Let's try to encourage Solver to keep that solution by setting its weight to 1.5
• The homing projectile having slow direct damage also seems like a good idea, so let's set that to 1.5 as well.
• The electric arc mechanism having AoE damage only seems silly; if this is going to bounce to 3 targets in sequence, there's no point having it be AoE damage only.  We'll set that to 0.

Our revised Weights Table, with all the changes we've made so far, now looks like this:

We re-solve, and get this output:

This is closer, but still no cigar; there are still some combinations that don't make sense.

For the sake of simplicity, I'll end this example here.  It shouldn't take too much longer to find a good set of towers.  You can easily download the spreadsheet and play around with the weights yourself; depending on what mechanism/effect combinations you prefer, any number of configurations will be valid.

If you're interested in how I solved it in my particular case, the design of the towers in City Conquest is a relatively close match.

Why It's Useful

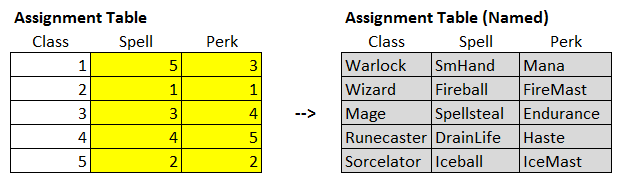
Some readers were confused by Part 5 in this series, since the example used in that article was intentionally preposterous.

By now, though, it should be clear what we were getting at.  Part 5 actually gave us a number of useful decision model archetypes for solving exactly these types of parametric design problems!

In Part 5, we were attempting to solve assignment problems between 2 or more classes of attributes (3 in the case of that particular example: classes, spells, and perks).  Solving that problem allowed us to build a simple framework that we could then generalize to solve assignment problems, which are exactly the same as the parametric design problems we're addressing here.

And it should be clear by now that using this kind of a disciplined approach can be much more useful than randomly guessing at the design of our towers (or enemies, or spells, or loot, or whatever parametric design problem we're facing for our particular game), since it allows us to much more easily design each element in the context of the whole, and we can very easily experiment with alternative design configurations by tweaking a few parts of the spreadsheet and hitting "Solve."

Generalizing

Now let's take our framework and generalize further.  In the attached spreadsheet, the second worksheet is labeled "Generic 2 Parameters;" you can modify this to serve as a template for these kinds of parametric design problems with 2 parameters.

This worksheet is nearly identical to the one we used in the tower defense problem above, with letters ('a'-'h') substituted for the tower attack mechanisms and random city names ("New York," "Boston," etc) substituted for the effects -- fill these in with whatever values apply to your problem.  We could also use numeric parameters here for things like weapon ranges, or stuff them into broad categories to allow us to enumerate them (i.e. "Short Range," "Medium Range," and "Long Range.")

The next worksheet in the spreadsheet is "Generic 3 Parameters," and it adds a third parameter category, which we fill in with arbitrary Greek letters to represent some arbitrary third dimension for our problem (just as with the "Spells / Perks / Classes" example in Part 5).

You can then easily create similar worksheets with 4, 5, or more parameters by adapting from the 3-parameter solution and tweaking it to suit your needs.

We also leave the implementation of problem-specific constraints as an exercise for the reader, since these constraints will inevitably be specific to the problem at hand.  Part 5 contains models broadly similar to those presented here, and it may offer some useful hints as to how to implement these types of constraints.

Conclusion

Even when the problem you're facing is not a numerical one, and even when there's no way for us to find an exact optimal solution, it should be clear by now that the exercise of taking a design problem and framing it as a decision problem can have huge benefits, because it can help you see the problem in a new way and experiment with alternatives much more quickly.

Although there's a bit of a learning curve involved, once you master that, decision modeling and optimization techniques can give you a whole new power tool to approach certain classes of design problems.  This process allows designers full control over the subjective aspects of the design, and uses Solver to help quickly iterate over the possibilities.

Over the course of this series, we've illustrated a number of ways to use this power tool.  We've had to slow down the pace of our posts due to other obligations, but this series is far from over.

Stay tuned!  In future articles, we'll do a deeper dive into finding an optimal build order in a turn-based strategy game such as Civilization, build decision models to help us design game levels and analyze game world layouts in a Metroid Prime style of game, and much more.



-Paul Tozour


This article was edited by Professor Christopher Thomas Ryan, Assistant Professor of Operations Management at the University of Chicago Booth School of Business.

Decision Modeling and Optimization in Game Design, Part 5: Class Assignment Problems

This article is the fifth in a continuing series on the use of decision modeling and optimization techniques for game design.  The full list of articles includes:

• Part 1: Introduction (Blogspot) (Gamasutra)
• Part 2: Optimization Basics and Unrolling a Simulation (Blogspot) (Gamasutra)
• Part 3: Allocation and Facility Location Problems (Blogspot) (Gamasutra)
• Part 4: Competitive Balancing Problems (Blogspot) (Gamasutra)
• Part 5: Class Assignment Problems (Blogspot) (Gamasutra)
• Part 6: Parametric Design Techniques (Blogspot) (Gamasutra)
• Part 7: Production Queues (Blogspot) (Gamasutra)
• Part 8: Graph Search (Blogspot) (Gamasutra)
• Part 9: Modular Level Design (Blogspot) (Gamasutra)

The spreadsheet for this article can be downloaded here: link

Introduction

In the previous articles in this series, we introduced the concepts behind decision modeling and optimization – a set of tools that can be helpful in framing and optimizing a surprising number of design decisions. We also discussed their limitations and showed a number of examples of how they can be used to find optimal player strategies in certain cases and to help optimize design decisions directly (see links above).

In this week’s update, we’ll introduce assignment problems and show some potential ways to solve this class of problems. Then we'll reveal the stunning plot twist, that this entire article has been an elaborate setup for the next episode, in which we’ll discuss some practical applications of these techniques and discuss how we used a similar approach to frame the building design problems in our recent iOS/Android game City Conquest.

The Problem

It’s your first day on the job at a company that designs massively-multiplayer role-playing games (MMORPGs). You’re very excited to start work on their new fantasy MMORPG, which has been in development for six months.

Upon arriving at work, you receive a long-distance Skype call from your boss, who has left for two months of intensive research in Tahiti.

“We’ve got a problem,” she explains. “We’ve just refactored our design. Totally changed everything – it wasn’t working out, so we smashed it to bits and restarted from scratch.”

“That’s cool,” you reply. “You guys warned me during the interview that you do a lot of design changes.”

“Yeah, we do. So the net result is, we’ve got an issue with the tier 2 spells for the spellcasting classes, and I’d like you to take a look at it. We have five character classes in the game that can cast spells. We also have five spells that aren’t assigned right now, and five ‘perks’ that are in design that seem like a good fit for spell-casting character classes. So I want you to figure out which classes get which spells and which perks.”

“Sounds easy enough,” you reply.

“See if you can take a shot at this,” she replies. “Here are the classes, spells, and perks:"

• Classes: Warlock, Wizard, Mage, Runecaster, Sorcelator
• Spells: Fireball, Iceball, SpellSteal, Drain Life, Smashing Hand
• Perks: Mana Regeneration, Endurance, Haste, Fire Mastery, Ice Mastery

“OK. How do you want me to go about doing these assignments?”

“Here’s the feedback I’ve gotten from the design team:

• It seems pretty obvious that the Fire Mastery and Ice Mastery perks should go with whatever classes get the Fireball and Iceball spells, respectively.
• We’d like the Warlock to get the Mana Regeneration perk.
• We haven’t figured out what spell the Wizard should get, but we do know that Iceball would not be a good fit for that class.
• We want the Runecaster to get the Drain Life spell.
• The Haste perk would not be appropriate for the Mage.
• The Mana Regeneration perk isn’t a good fit for the class that ends up getting the Spellsteal spell.
• We want to make sure the Mage does not get the Fireball or Iceball spells.”

“OK, boss,” you reply. “I’ve got all that written down.”

“I honestly don’t know if there’s a way of assigning these that even works,” she continues. “It might not even be possible. Alternatively, there might be more than one way to assign it that makes it work. I just don’t know. What do you think?”

Think about this problem for a moment. How would you solve this? And how many solutions are there – zero, one, or more than one?

It’s Tougher Than it Looks

This is a difficult problem. Unlike most of the problems in this series, though, it’s one that you can, in fact, solve by hand (where by “solve” I mean that you can find a feasible solution – in this case, there is only one).

If you've ever solved a classical logic puzzle, you might recognize this problem. Most of these take the form of figuring out the correct assignments of objects. For example, you have to figure out which of N people wore N hats of N colors to a certain party.

In order to solve these kinds of logic puzzles, you typically make a matrix of adjoining NxN tables, with one table for each permutation of two categories. Then you fill them in with everything you know about the problem, and then try to solve them using inference, almost like Sudoku puzzles. You fill in an assignment you know to be correct with an ‘o’ and an assignment you know to be incorrect with an ‘x,’ and then you can use basic rules of logic to fill in the entire table.

For example, each ‘o’ you place in a part of the table allows you to fill in all cells in the same row and column with an ‘x,’ since there is only one possible assignment. Similarly, if any given row or column of an NxN subtable is filled with ‘x’ values except for one cell, you can fill that empty cell with an ‘o,’ since by process of elimination, the one remaining cell must be the valid assignment.

(There are some good examples online at http://www.printable-puzzles.com/printable-logic-puzzles.php, and you can see tips on solving them at http://www.puzzlersparadise.com/article1021.html and http://www.youtube.com/watch?v=CNxfZwvaQ-k.)

Since the problem we’re trying to solve is assigning N classes to N spells to N perks, where N=5, we’ll need a set of 3 adjoining 5x5 tables, one each for all of the possible [classes, spells], [classes, perks], and [perks, spells] assignments. Here’s what that would look like in our case: we have a [classes, perks] table (in peach, at the top), a [classes, spells] table (bottom left), and a [perks, spells] table (bottom right).

In order to get the ball rolling, we’ve already started filling in the table with the constraints from the problem description. We fill in an ‘O’ in any cell where we know that the assignment must hold, and an ‘X’ in any cell where we know an assignment is forbidden.

In this case, the boss’ insistence that the Fire Mastery and Ice Mastery perks should go with the Fireball and Iceball spells made us put the two ‘O’ cells in the green perks/spells table in the lower right, one correlating Fire Mastery with Fireball and the other correlating Ice Mastery with Iceball. The ‘X’ just below and to the right of those, denying a correlation between Mana Regeneration and SpellSteal, encapsulates the boss’ insistence that the Mana Regeneration perk isn’t a good fit for the class that ends up getting the Spellsteal spell. If you read through all of the other constraints listed, you’ll see that the table above encapsulates them precisely.

The next step is to make as many inferences as we can from that point. For every cell with an ‘O,’ we know that no other cell in that row or column in that sub-table can have an ‘O.’ Therefore, we can fill them in with ‘X’ marks.

For example, we’ve filled in the ‘O’ in the upper left (peach) sub-table indicating that the Warlock gets the Mana Regeneration perk. Therefore, no other class can get Mana Regeneration, and the Warlock cannot have any other perk. Once we fill in all of those ‘X’ marks, we get a table that looks like this:

That’s a lot better! Now we can instantly see what assignments can’t be possible, and this can give us a much better handle on what can be possible. We can also use a few other basic rules of logic to complete this puzzle – for example, if there are four ‘X’ marks in any row or column, and the fifth cell in that row or column is blank, then we know by process of elimination that there must be an ‘O’ there. Luckily, the step above nearly filled in the “Iceball” row in the blue spells/classes assignment table in the lower left, so if we can rule out either the Warlock or the Sorcelator for Iceball, we can fill in the other class.

We can also use basic logical inference to help us fill in more. For example, we can see that the Warlock has Mana Regeneration, and the spells/perks table in the lower right (green) shows that we have ‘X’ marks in the “Mana Regen” column for Iceball and SpellSteal. This means that we can go to the spells/classes table in the lower left (blue) and fill in ‘X’ marks in the Warlock column for Iceball and SpellSteal.

Which, of course, from our inference in the prior paragraph, means that the Sorcelator must be the one who gets Iceball …

But instead of completing the exercise in that way, we’re going to stop there and change course. Curious readers are welcome to try to solve this puzzle by hand – it’s not too difficult from this point – but taking the manual exercise any further would be a waste of time. After all, this series is all about automated decision modeling. We’re all about getting computers to do the heavy lifting for us, not filling in big tables by hand.

So instead of trying to find the solution manually, let’s see if there’s a way we can frame this as a decision modeling problem in Excel. Even though this is obviously a toy problem, there’s surely something we can learn from this.

Design Wizard Casts “Summon Decision Model”

Ideally, we could somehow take this table and import it whole-hog into Excel, and then let Excel figure out whether to fill in each cell with an ‘X’ or an ‘O.’ Unfortunately, trying to do it in a single unified table is a bit messy – Solver is going to want us to specify our decision cells (and set the optimization constraints on them) in a small number of rectangular sections on the grid, and this won’t mesh nicely with all those cells with fixed ‘X’ and ‘O’ values.

Instead of that, we’re going to break it up into three different tables: one for the constraints stated in the problem, a second table for the decision cells to optimize, and a third table that will combine the two.

First, we make the “constraint table,” as shown below. This table is exactly the same shape as our manual logic puzzle, but we fill in each cell with either ‘1’ to indicate an ‘O’ value, ‘0’ (zero) to indicate an ‘X’ value, or ‘-1’ to indicate that the value of the cell isn’t stated in the problem definition.

Next, we’ll make a separate table for the decision variables. This table will be the one we optimize with Solver. We’ll fill in each cell with 0 to start out, and we’ll ensure that Solver sets each cell to either 0 or 1.

Finally, we’ll make a third table that combines both of these two: the “combined output table.” This table will combine the values of the “constraint table” and the decision cells together. Each cell in this third table will use the value in the “constraint table” if it is 0 or 1, but if it’s -1 (meaning it’s not explicitly defined in the problem statement), it will use the value from the (yellow) decision variable table instead. Each cell in this combined output table will serve as the actual, final value.

We will also use special counter cells around the outer edges to determine how many cells in each row or column of each sub-table are set to a value of ‘1.’ We know that the final solution should have exactly a single assignment for each combination, so it should have exactly one ‘1’ value in each row and column of each of the three sub-tables, so we know that these summation cells should have a final value of 1.

Here’s what the combined output table looks like:

The grey cells around the left, right, top, and bottom are the summation cells – as you can see, they each count the total of the cells in the nearest row or column of the nearest sub-table. We use these to count the number of times each element is used. Once we’ve found the proper assignments, all of these grey cells should equal 1, to indicate that there’s been exactly five non-conflicting [spell, class] assignment, exactly five non-conflicting [class, perk] assignments, and exactly five non-conflicting [spell, perk] assignments.

The two purple cells in the lower left calculate the sum of the left-hand column and the bottom row of the summation cells. We know that once all of the tables are filled in, each of these should have a value of 10, since each of the 10 cells of the left-hand column and the bottom row should have a value of 1.

The orange objective cell at the bottom simply adds the values of the two purple cells.

Now, we solve!

• The cell in the “Set Objective” category is the orange objective cell, and we try to maximize its value (we could set it to “Value Of”=20 knowing that its value cannot exceed 20, but in practice, this is less reliable than simply maximizing it, since it can’t physically go over 20 anyway).

• The cell ranges in the “By Changing Variable Cells” category are our yellow decision cells in the binary decision variable table.

• The two “…=binary” constraints are constraints on our decision cells. Setting a “binary” constraint ensures that the Solver will force each cell in the range to a value of either 0 or 1, which is exactly what we want.

• All the remaining constraints are “…=1” constraints, and these are constraints on the four greyed summation categories above, below, left, and right of our final combined output table. This will ensure that we have exactly one assignment for each class to each spell, each class to each perk, and each spell to each perk.

• We set to the “Evolutionary” solving method, since the other solvers cannot handle a problem like this.

Now run it! Within 5-10 seconds, we should get a table that looks like this:

Problem solved, right?

Well … no.  Not exactly.

The three tables are all “solved,” but they’ve been solved independently, so they don’t necessarily make any sense as a whole. The left side of the table shows that the Warlock has the Mana Regeneration perk and the Iceball spell, but the spells/perks table on the right shows that whoever has the Iceball spell should actually have Ice Mastery instead. Similarly, the Wizard has the Haste Perk and the Smashing Hand spell, but the spells/perks table on the right shows that whoever has Smashing Hand should have Mana Regeneration.

In other words, we’ve only implemented a partial solution, because we’ve solved the three sub-tables ([class,perk], [perk,spell], and [class, spell]) separately, and they need to be solved together.

This is a problem! There’s surely some way to fix it, but it would require us to do seriously complex Excel mojo to try to add constraints that would properly correlate across all three tables.

Instead of doing that, let’s see if we can’t find a simpler way to represent the entire problem.

Design Sorcelator Targets Decision Model and Casts “Simplify”

Instead of trying to build a huge table and optimize it, let’s see if we can’t find a much simpler representation. After all, each class should have only one spell and one perk, so we should be able to just set up a “spell” entry and a “perk” entry for each of the 5 classes. Then, we can hold the classes fixed, and try to optimize the 1 spell and 1 perk that belong to each the 5 classes, so that we end up optimizing a total of only 10 decision cells, instead of the 75 yellow decision cells from the previous decision model.

We’ll start by making three tables, listing the classes, spells, and perks.

These five tables indicate numerical assignments: we’ll use the digits 1 through 5 to represent each of the 5 classes, spells, and perks. These tables indicate which class, spell, or perk a given number stands for, depending on where it’s used.

Next, we’ll set up an “assignment table” listing a spell and a perk for each class, with each one represented by a number between 1 and 5 corresponding to the appropriate entry in the tables above. This is shown below.

This table shows the current assignments. Each row represents one class (these five are held fixed), and the corresponding “Spell” and “Perk” columns represent the spell and perk currently assigned to that class. Once we find the optimal values for these ten yellow decision cells, we’ll have found the five [class, spell, perk] assignments that correctly satisfy our problem criteria, and each of the “Spell” and “Perk” columns should contain each of the digits ‘1’ through ‘5’ in some order.

As you can see, the cells on the left (in the “Class” column of the Assignment Table) are uncolored, since we don’t need to change the ordering of the classes; we just need to determine the values of the other two relative to the classes.

The table just to the right (“Assignment Table (Named)”) just shows the names of the classes, spells, and perks of the table on the left. It contains Excel functions that translate the numbers in the Assignment Table into text descriptions using the lookup tables at the beginning of this section (so that, for example, the first row shows we are giving the Warlock the Fireball spell and Mana Regeneration perk with this initial setup).

This table neatly encapsulates the [class, spell] and [class, perk] subsections of the logic matrix we prepared at the beginning of this article (the red and blue sub-tables along the left side of the matrix). However, it doesn’t encapsulate the [spell, perk] mappings at all (the green sub-table at the lower right corner of the logic matrix). This is a problem, since several of the elements in our problem statement (our constraints) are in the form of mappings between perks and spells, with no mention of classes. So with the way the Assignment Table is currently set up, we can’t set up constraints relating to [spell, perk] mappings without testing every pair in the list – and that seems like it could get messy.

Instead, we’ll set up a simple table like the one below, that maps each [spell, perk] combination to a number, by treating the spell as the “tens” digit and the perk as the “ones” digit.

In this way, we can easily set up constraints that search through this table to see if any given [spell, perk] combination does or does not exist.

We also need to ensure that when we optimize our decision cells, we end up with exactly one of each of the values ‘1,’ ‘2,’ ‘3,’ ‘4,’ and ‘5’ in the “Spell” and “Perk” columns of the Assignment Table. This would be easy to do if Excel had a good function for ensuring that all the cells in a given range had unique values, but unfortunately, it does not. Solver also has a special “dif” constraint type that is supposed to ensure this uniqueness, but it unfortunately comes with its own set of idiosyncrasies that makes it more or less useless for our purposes.

Therefore, in order to ensure that we end up with exactly those five values (in any order), we’ll set up a special “Uniqueness Detector” table that detects the presence of ‘1,’ ‘2,’ ‘3,’ etc values in each of the “Spell” and “Perk” columns of the Assignment table. They do this by calling the MATCH() Excel function (and then wrapping it in an ISNA() function since MATCH() returns the special value “#N/A” when the value is not found).

Finally, we set up a table to test our constraints. Our approach in this case is rather unique; we explicitly set up a cell for every constraint as its own separate entry that will have a value of ‘1’ when the constraint is satisfied and ‘0’ otherwise. Each of these cells (the grey cells in the table below) tests one of the conditions in the problem description.

A few quick notes on the setup of these constraint cells:

• The constraints related to [class, spell] and [class, perk] mappings are trivial; they just use the Excel “IF()” function to test a certain condition in the Assignment Table (the decision cells).

• The constraints related to [spell, perk] mappings instead query the special “Spells-to-Perks Table” we set up earlier. Just as in our “Uniqueness counter” table, they use the Excel “MATCH()” function to try to test for the presence or absence of a certain [spell, perk] combination anywhere in that table, and then wrap this inside Excel’s ISNA() function to test for the special return value “#N/A” if the value is not found.

• Finally, the last two cells ensure that each perk and each spell is used exactly once. They do this by simply summing up each respective column of the “Uniqueness counter” table we set up earlier; if the “Spells” column of the Assignment Table contains the values ‘1’ through ‘5’ in any order, then the “Spells” column of the Uniqueness counter should all have ‘1’ values and should have a total of 5 (and similarly for the “Perks” column of each of those two tables).

Finally, the orange objective cell at the bottom adds up the total number of satisfied constraints. This is different from the objective functions we’ve used so far; we’ve generally been trying to minimize or maximize some value, but in this case, we're simply trying to ensure that all the constraints are satisfied.  Any solution that satisfies all the constraints is a "correct" answer, so we can just count the number of properly satisfied constraints and use that as the objective value.

Now that we’ve got all that out of the way, we’re ready to run Solver:

We target the orange objective cell, as always, and try to maximize its value (knowing it can never go beyond 10). In “By Changing Variable Cells,” we enter the cell range for our Assignment Table (including both the blue and yellow cells). These are our decision cells. Finally, we add three Solver constraints to tell it that all the cells in the Assignment Table must be integers between 1 and 5, inclusive.

Finally, we ensure that “Solving Method” is set to “Evolutionary,” and hit Solve. It can be time-consuming, as this is a non-trivial problem; it can take 30-60 seconds for the objective cell to get up to a value of 10 indicating that all 10 constraints have been met.

Here's the final, correct solution:

And there you have it! These tables show the numeric and text versions of the final solution, respectively. We could pretty much take the table on the right, e-mail it to the boss, and call it a day.

[You can download the spreadsheet for this article here; note the each example is in a different worksheet.]

Congratulations! You Have Reached Level 5. Your Stamina has increased by 2.

“Well,” you might find yourself thinking, “That was long, and really ridiculous. You set up an obvious toy problem that was basically a thinly disguised logic puzzle. That situation would obviously never happen in real life. Then you went through a whole lot of complicated spreadsheet wrangling to finally solve it when you could have just done the whole thing by hand in ten minutes!”

All true. Guilty as charged!

But the point, of course, is not about what classes get what spells, it’s about how we can apply this kind of decision model in all kinds of useful ways you might never have imagined. The journey is far more important than the destination, and this particular kind of journey is one we face as designers in many different forms.

In the next episode, I’ll delve into a much more practical example and show how we used a similar approach to design the towers and dropship pads in our iOS/Android game, City Conquest.


-Paul Tozour

Part 6 in this series is now available here.

Please note that we have switched to a bi-weekly posting schedule due to time constraints.

This article was edited by Professor Christopher Thomas Ryan, Assistant Professor of Operations Management at the University of Chicago Booth School of Business