Sunday, August 11, 2013

Decision Modeling and Optimization in Game Design, Part 5: Class Assignment Problems

This article is the fifth in a continuing series on the use of decision modeling and optimization techniques for game design.  The full list of articles includes:


The spreadsheet for this article can be downloaded here: link


Introduction

In the previous articles in this series, we introduced the concepts behind decision modeling and optimization – a set of tools that can be helpful in framing and optimizing a surprising number of design decisions. We also discussed their limitations and showed a number of examples of how they can be used to find optimal player strategies in certain cases and to help optimize design decisions directly (see links above).

In this week’s update, we’ll introduce assignment problems and show some potential ways to solve this class of problems. Then we'll reveal the stunning plot twist, that this entire article has been an elaborate setup for the next episode, in which we’ll discuss some practical applications of these techniques and discuss how we used a similar approach to frame the building design problems in our recent iOS/Android game City Conquest.

The Problem

It’s your first day on the job at a company that designs massively-multiplayer role-playing games (MMORPGs). You’re very excited to start work on their new fantasy MMORPG, which has been in development for six months.

Upon arriving at work, you receive a long-distance Skype call from your boss, who has left for two months of intensive research in Tahiti.

“We’ve got a problem,” she explains. “We’ve just refactored our design. Totally changed everything – it wasn’t working out, so we smashed it to bits and restarted from scratch.”

“That’s cool,” you reply. “You guys warned me during the interview that you do a lot of design changes.”

“Yeah, we do. So the net result is, we’ve got an issue with the tier 2 spells for the spellcasting classes, and I’d like you to take a look at it. We have five character classes in the game that can cast spells. We also have five spells that aren’t assigned right now, and five ‘perks’ that are in design that seem like a good fit for spell-casting character classes. So I want you to figure out which classes get which spells and which perks.”

“Sounds easy enough,” you reply.

“See if you can take a shot at this,” she replies. “Here are the classes, spells, and perks:"

  • Classes: Warlock, Wizard, Mage, Runecaster, Sorcelator
  • Spells: Fireball, Iceball, SpellSteal, Drain Life, Smashing Hand
  • Perks: Mana Regeneration, Endurance, Haste, Fire Mastery, Ice Mastery

“OK. How do you want me to go about doing these assignments?”

“Here’s the feedback I’ve gotten from the design team:

  • It seems pretty obvious that the Fire Mastery and Ice Mastery perks should go with whatever classes get the Fireball and Iceball spells, respectively.
  • We’d like the Warlock to get the Mana Regeneration perk.
  • We haven’t figured out what spell the Wizard should get, but we do know that Iceball would not be a good fit for that class.
  • We want the Runecaster to get the Drain Life spell.
  • The Haste perk would not be appropriate for the Mage.
  • The Mana Regeneration perk isn’t a good fit for the class that ends up getting the Spellsteal spell.
  • We want to make sure the Mage does not get the Fireball or Iceball spells.”

“OK, boss,” you reply. “I’ve got all that written down.”

“I honestly don’t know if there’s a way of assigning these that even works,” she continues. “It might not even be possible. Alternatively, there might be more than one way to assign it that makes it work. I just don’t know. What do you think?”

Think about this problem for a moment. How would you solve this? And how many solutions are there – zero, one, or more than one?

It’s Tougher Than it Looks

This is a difficult problem. Unlike most of the problems in this series, though, it’s one that you can, in fact, solve by hand (where by “solve” I mean that you can find a feasible solution – in this case, there is only one).

If you've ever solved a classical logic puzzle, you might recognize this problem. Most of these take the form of figuring out the correct assignments of objects. For example, you have to figure out which of N people wore N hats of N colors to a certain party.

In order to solve these kinds of logic puzzles, you typically make a matrix of adjoining NxN tables, with one table for each permutation of two categories. Then you fill them in with everything you know about the problem, and then try to solve them using inference, almost like Sudoku puzzles. You fill in an assignment you know to be correct with an ‘o’ and an assignment you know to be incorrect with an ‘x,’ and then you can use basic rules of logic to fill in the entire table.

For example, each ‘o’ you place in a part of the table allows you to fill in all cells in the same row and column with an ‘x,’ since there is only one possible assignment. Similarly, if any given row or column of an NxN subtable is filled with ‘x’ values except for one cell, you can fill that empty cell with an ‘o,’ since by process of elimination, the one remaining cell must be the valid assignment.

(There are some good examples online at http://www.printable-puzzles.com/printable-logic-puzzles.php, and you can see tips on solving them at http://www.puzzlersparadise.com/article1021.html and http://www.youtube.com/watch?v=CNxfZwvaQ-k.)

Since the problem we’re trying to solve is assigning N classes to N spells to N perks, where N=5, we’ll need a set of 3 adjoining 5x5 tables, one each for all of the possible [classes, spells], [classes, perks], and [perks, spells] assignments. Here’s what that would look like in our case: we have a [classes, perks] table (in peach, at the top), a [classes, spells] table (bottom left), and a [perks, spells] table (bottom right).




In order to get the ball rolling, we’ve already started filling in the table with the constraints from the problem description. We fill in an ‘O’ in any cell where we know that the assignment must hold, and an ‘X’ in any cell where we know an assignment is forbidden.

In this case, the boss’ insistence that the Fire Mastery and Ice Mastery perks should go with the Fireball and Iceball spells made us put the two ‘O’ cells in the green perks/spells table in the lower right, one correlating Fire Mastery with Fireball and the other correlating Ice Mastery with Iceball. The ‘X’ just below and to the right of those, denying a correlation between Mana Regeneration and SpellSteal, encapsulates the boss’ insistence that the Mana Regeneration perk isn’t a good fit for the class that ends up getting the Spellsteal spell. If you read through all of the other constraints listed, you’ll see that the table above encapsulates them precisely.

The next step is to make as many inferences as we can from that point. For every cell with an ‘O,’ we know that no other cell in that row or column in that sub-table can have an ‘O.’ Therefore, we can fill them in with ‘X’ marks.

For example, we’ve filled in the ‘O’ in the upper left (peach) sub-table indicating that the Warlock gets the Mana Regeneration perk. Therefore, no other class can get Mana Regeneration, and the Warlock cannot have any other perk. Once we fill in all of those ‘X’ marks, we get a table that looks like this:



That’s a lot better! Now we can instantly see what assignments can’t be possible, and this can give us a much better handle on what can be possible. We can also use a few other basic rules of logic to complete this puzzle – for example, if there are four ‘X’ marks in any row or column, and the fifth cell in that row or column is blank, then we know by process of elimination that there must be an ‘O’ there. Luckily, the step above nearly filled in the “Iceball” row in the blue spells/classes assignment table in the lower left, so if we can rule out either the Warlock or the Sorcelator for Iceball, we can fill in the other class.

We can also use basic logical inference to help us fill in more. For example, we can see that the Warlock has Mana Regeneration, and the spells/perks table in the lower right (green) shows that we have ‘X’ marks in the “Mana Regen” column for Iceball and SpellSteal. This means that we can go to the spells/classes table in the lower left (blue) and fill in ‘X’ marks in the Warlock column for Iceball and SpellSteal.

Which, of course, from our inference in the prior paragraph, means that the Sorcelator must be the one who gets Iceball …

But instead of completing the exercise in that way, we’re going to stop there and change course. Curious readers are welcome to try to solve this puzzle by hand – it’s not too difficult from this point – but taking the manual exercise any further would be a waste of time. After all, this series is all about automated decision modeling. We’re all about getting computers to do the heavy lifting for us, not filling in big tables by hand.

So instead of trying to find the solution manually, let’s see if there’s a way we can frame this as a decision modeling problem in Excel. Even though this is obviously a toy problem, there’s surely something we can learn from this.

Design Wizard Casts “Summon Decision Model”

Ideally, we could somehow take this table and import it whole-hog into Excel, and then let Excel figure out whether to fill in each cell with an ‘X’ or an ‘O.’ Unfortunately, trying to do it in a single unified table is a bit messy – Solver is going to want us to specify our decision cells (and set the optimization constraints on them) in a small number of rectangular sections on the grid, and this won’t mesh nicely with all those cells with fixed ‘X’ and ‘O’ values.

Instead of that, we’re going to break it up into three different tables: one for the constraints stated in the problem, a second table for the decision cells to optimize, and a third table that will combine the two.

First, we make the “constraint table,” as shown below. This table is exactly the same shape as our manual logic puzzle, but we fill in each cell with either ‘1’ to indicate an ‘O’ value, ‘0’ (zero) to indicate an ‘X’ value, or ‘-1’ to indicate that the value of the cell isn’t stated in the problem definition.



Next, we’ll make a separate table for the decision variables. This table will be the one we optimize with Solver. We’ll fill in each cell with 0 to start out, and we’ll ensure that Solver sets each cell to either 0 or 1.



Finally, we’ll make a third table that combines both of these two: the “combined output table.” This table will combine the values of the “constraint table” and the decision cells together. Each cell in this third table will use the value in the “constraint table” if it is 0 or 1, but if it’s -1 (meaning it’s not explicitly defined in the problem statement), it will use the value from the (yellow) decision variable table instead. Each cell in this combined output table will serve as the actual, final value.

We will also use special counter cells around the outer edges to determine how many cells in each row or column of each sub-table are set to a value of ‘1.’ We know that the final solution should have exactly a single assignment for each combination, so it should have exactly one ‘1’ value in each row and column of each of the three sub-tables, so we know that these summation cells should have a final value of 1.

Here’s what the combined output table looks like:



The grey cells around the left, right, top, and bottom are the summation cells – as you can see, they each count the total of the cells in the nearest row or column of the nearest sub-table. We use these to count the number of times each element is used. Once we’ve found the proper assignments, all of these grey cells should equal 1, to indicate that there’s been exactly five non-conflicting [spell, class] assignment, exactly five non-conflicting [class, perk] assignments, and exactly five non-conflicting [spell, perk] assignments.

The two purple cells in the lower left calculate the sum of the left-hand column and the bottom row of the summation cells. We know that once all of the tables are filled in, each of these should have a value of 10, since each of the 10 cells of the left-hand column and the bottom row should have a value of 1.

The orange objective cell at the bottom simply adds the values of the two purple cells.

Now, we solve!



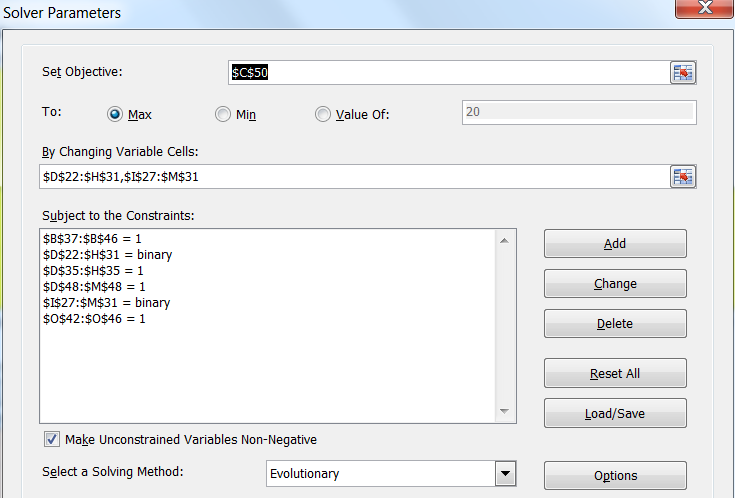
  • The cell in the “Set Objective” category is the orange objective cell, and we try to maximize its value (we could set it to “Value Of”=20 knowing that its value cannot exceed 20, but in practice, this is less reliable than simply maximizing it, since it can’t physically go over 20 anyway).
  • The cell ranges in the “By Changing Variable Cells” category are our yellow decision cells in the binary decision variable table.
  • The two “…=binary” constraints are constraints on our decision cells. Setting a “binary” constraint ensures that the Solver will force each cell in the range to a value of either 0 or 1, which is exactly what we want.
  • All the remaining constraints are “…=1” constraints, and these are constraints on the four greyed summation categories above, below, left, and right of our final combined output table. This will ensure that we have exactly one assignment for each class to each spell, each class to each perk, and each spell to each perk.
  • We set to the “Evolutionary” solving method, since the other solvers cannot handle a problem like this.

Now run it! Within 5-10 seconds, we should get a table that looks like this:



Problem solved, right?

Well … no.  Not exactly.

The three tables are all “solved,” but they’ve been solved independently, so they don’t necessarily make any sense as a whole. The left side of the table shows that the Warlock has the Mana Regeneration perk and the Iceball spell, but the spells/perks table on the right shows that whoever has the Iceball spell should actually have Ice Mastery instead. Similarly, the Wizard has the Haste Perk and the Smashing Hand spell, but the spells/perks table on the right shows that whoever has Smashing Hand should have Mana Regeneration.

In other words, we’ve only implemented a partial solution, because we’ve solved the three sub-tables ([class,perk], [perk,spell], and [class, spell]) separately, and they need to be solved together.

This is a problem! There’s surely some way to fix it, but it would require us to do seriously complex Excel mojo to try to add constraints that would properly correlate across all three tables.

Instead of doing that, let’s see if we can’t find a simpler way to represent the entire problem.


Design Sorcelator Targets Decision Model and Casts “Simplify”


Instead of trying to build a huge table and optimize it, let’s see if we can’t find a much simpler representation. After all, each class should have only one spell and one perk, so we should be able to just set up a “spell” entry and a “perk” entry for each of the 5 classes. Then, we can hold the classes fixed, and try to optimize the 1 spell and 1 perk that belong to each the 5 classes, so that we end up optimizing a total of only 10 decision cells, instead of the 75 yellow decision cells from the previous decision model.

We’ll start by making three tables, listing the classes, spells, and perks.




These five tables indicate numerical assignments: we’ll use the digits 1 through 5 to represent each of the 5 classes, spells, and perks. These tables indicate which class, spell, or perk a given number stands for, depending on where it’s used.

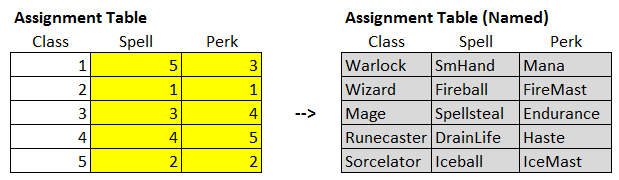
Next, we’ll set up an “assignment table” listing a spell and a perk for each class, with each one represented by a number between 1 and 5 corresponding to the appropriate entry in the tables above. This is shown below.



This table shows the current assignments. Each row represents one class (these five are held fixed), and the corresponding “Spell” and “Perk” columns represent the spell and perk currently assigned to that class. Once we find the optimal values for these ten yellow decision cells, we’ll have found the five [class, spell, perk] assignments that correctly satisfy our problem criteria, and each of the “Spell” and “Perk” columns should contain each of the digits ‘1’ through ‘5’ in some order.

As you can see, the cells on the left (in the “Class” column of the Assignment Table) are uncolored, since we don’t need to change the ordering of the classes; we just need to determine the values of the other two relative to the classes.

The table just to the right (“Assignment Table (Named)”) just shows the names of the classes, spells, and perks of the table on the left. It contains Excel functions that translate the numbers in the Assignment Table into text descriptions using the lookup tables at the beginning of this section (so that, for example, the first row shows we are giving the Warlock the Fireball spell and Mana Regeneration perk with this initial setup).

This table neatly encapsulates the [class, spell] and [class, perk] subsections of the logic matrix we prepared at the beginning of this article (the red and blue sub-tables along the left side of the matrix). However, it doesn’t encapsulate the [spell, perk] mappings at all (the green sub-table at the lower right corner of the logic matrix). This is a problem, since several of the elements in our problem statement (our constraints) are in the form of mappings between perks and spells, with no mention of classes. So with the way the Assignment Table is currently set up, we can’t set up constraints relating to [spell, perk] mappings without testing every pair in the list – and that seems like it could get messy.

Instead, we’ll set up a simple table like the one below, that maps each [spell, perk] combination to a number, by treating the spell as the “tens” digit and the perk as the “ones” digit.



In this way, we can easily set up constraints that search through this table to see if any given [spell, perk] combination does or does not exist.

We also need to ensure that when we optimize our decision cells, we end up with exactly one of each of the values ‘1,’ ‘2,’ ‘3,’ ‘4,’ and ‘5’ in the “Spell” and “Perk” columns of the Assignment Table. This would be easy to do if Excel had a good function for ensuring that all the cells in a given range had unique values, but unfortunately, it does not. Solver also has a special “dif” constraint type that is supposed to ensure this uniqueness, but it unfortunately comes with its own set of idiosyncrasies that makes it more or less useless for our purposes.

Therefore, in order to ensure that we end up with exactly those five values (in any order), we’ll set up a special “Uniqueness Detector” table that detects the presence of ‘1,’ ‘2,’ ‘3,’ etc values in each of the “Spell” and “Perk” columns of the Assignment table. They do this by calling the MATCH() Excel function (and then wrapping it in an ISNA() function since MATCH() returns the special value “#N/A” when the value is not found).



Finally, we set up a table to test our constraints. Our approach in this case is rather unique; we explicitly set up a cell for every constraint as its own separate entry that will have a value of ‘1’ when the constraint is satisfied and ‘0’ otherwise. Each of these cells (the grey cells in the table below) tests one of the conditions in the problem description.



A few quick notes on the setup of these constraint cells:

  • The constraints related to [class, spell] and [class, perk] mappings are trivial; they just use the Excel “IF()” function to test a certain condition in the Assignment Table (the decision cells).

  • The constraints related to [spell, perk] mappings instead query the special “Spells-to-Perks Table” we set up earlier. Just as in our “Uniqueness counter” table, they use the Excel “MATCH()” function to try to test for the presence or absence of a certain [spell, perk] combination anywhere in that table, and then wrap this inside Excel’s ISNA() function to test for the special return value “#N/A” if the value is not found.

  • Finally, the last two cells ensure that each perk and each spell is used exactly once. They do this by simply summing up each respective column of the “Uniqueness counter” table we set up earlier; if the “Spells” column of the Assignment Table contains the values ‘1’ through ‘5’ in any order, then the “Spells” column of the Uniqueness counter should all have ‘1’ values and should have a total of 5 (and similarly for the “Perks” column of each of those two tables).

Finally, the orange objective cell at the bottom adds up the total number of satisfied constraints. This is different from the objective functions we’ve used so far; we’ve generally been trying to minimize or maximize some value, but in this case, we're simply trying to ensure that all the constraints are satisfied.  Any solution that satisfies all the constraints is a "correct" answer, so we can just count the number of properly satisfied constraints and use that as the objective value.

Now that we’ve got all that out of the way, we’re ready to run Solver:



We target the orange objective cell, as always, and try to maximize its value (knowing it can never go beyond 10). In “By Changing Variable Cells,” we enter the cell range for our Assignment Table (including both the blue and yellow cells). These are our decision cells. Finally, we add three Solver constraints to tell it that all the cells in the Assignment Table must be integers between 1 and 5, inclusive.

Finally, we ensure that “Solving Method” is set to “Evolutionary,” and hit Solve. It can be time-consuming, as this is a non-trivial problem; it can take 30-60 seconds for the objective cell to get up to a value of 10 indicating that all 10 constraints have been met.

Here's the final, correct solution:



And there you have it! These tables show the numeric and text versions of the final solution, respectively. We could pretty much take the table on the right, e-mail it to the boss, and call it a day.

[You can download the spreadsheet for this article here; note the each example is in a different worksheet.]

Congratulations! You Have Reached Level 5. Your Stamina has increased by 2.

“Well,” you might find yourself thinking, “That was long, and really ridiculous. You set up an obvious toy problem that was basically a thinly disguised logic puzzle. That situation would obviously never happen in real life. Then you went through a whole lot of complicated spreadsheet wrangling to finally solve it when you could have just done the whole thing by hand in ten minutes!”

All true. Guilty as charged!

But the point, of course, is not about what classes get what spells, it’s about how we can apply this kind of decision model in all kinds of useful ways you might never have imagined. The journey is far more important than the destination, and this particular kind of journey is one we face as designers in many different forms.

In the next episode, I’ll delve into a much more practical example and show how we used a similar approach to design the towers and dropship pads in our iOS/Android game, City Conquest.


-Paul Tozour

Part 6 in this series is now available here.

 Please note that we have switched to a bi-weekly posting schedule due to time constraints.

This article was edited by Professor Christopher Thomas Ryan, Assistant Professor of Operations Management at the University of Chicago Booth School of Business
Posted by at
Labels:

No comments:

Post a Comment

Note: Only a member of this blog may post a comment.

Subscribe to: Post Comments (Atom)